AC-GAN Learns a Biased Distribution
Recently, I did a few small experiments to verify my hypothesis that the Auxiliary Classifier Generative Adversarial Network (AC-GAN) model has a particular down-sampling behavior. The goal of this post is to share some of the experiments I conducted while playing with AC-GAN.
What is AC-GAN?
First and foremost, we need to know what AC-GAN is. The Auxiliary Classifier Generative Adversarial Network (AC-GAN) is a GAN variant proposed by Odena, et al. in their 2017 ICML paper. Now, let \(p^*(x, y)\) denote the true image-label joint distribution and let \(p\_\theta(x, y)\) denote the generator joint distribution. In the AC-GAN paper, the objective functions are succinctly summarized as
\[\begin{align*} L_s &= \E_{p^*(x)} \brac{\ln D_\psi(x)} + \E_{p_\theta(x)}\brac{ \ln (1 - D_\psi(x))} \\ L_c &= \E_{p^*(x, y)}\brac{\ln q_\phi(y \mid x)} + \E_{p_\theta(x, y)}\brac{\ln q_\phi(y \mid x)} \end{align*}\]where \(D\_\psi\) is the discriminator, \(p\_\theta\) is the generator, and \(q\_\phi\) is the auxiliary classifier. The paper further proposes to share parameters between \(D\_\psi\) and \(q\_\phi\) by compressing both into a two-in-one neural network. The mini-max game played between the discriminator and generator is thus approximated by training the discriminator/auxiliary classifier to maximize \(L_c + L_s\) and training the generator to maximize \(L_c - L_s\).
Personally, I’m not a big fan of this presentation. The interaction resulting from parameter-sharing between the discriminator and auxiliary classifier is especially tricky to characterize. To make our lives simpler, it’s best to think of the discriminator and auxiliary classifier as two separate objects that, optionally, share neural network parameters for the sake of convenience. Furthermore, by noting that the alternating game is really just so that the discriminator loss approximates the Jensen-Shannon divergence (up to a constant), I think we’re better off describing the objective function that we’re minimizing w.r.t. \((\theta, \phi)\) as
\[\begin{align*} d(p^*(x), p_\theta(x)) - \E_{p^*(x, y)}\brac{\ln q_\phi(y \mid x)} - \E_{p_\theta(x, y)}\brac{\ln q_\phi(y \mid x)}, \end{align*}\]where \(d(\cdot, \cdot)\) denotes the JS divergence. From here on out, I shall refer to this as the AC-GAN objecitve function. I like this formulation better as it exposes the underlying machinery of the AC-GAN model and better illustrates the purpose of the auxiliary classifier. The first term is your standard GAN objective for training the generator. The second term ensures that the auxiliary classifier is trained to approximate the true posterior \(p^*(y \mid x)\). Once \(q_\phi\) is trained to become a sufficiently good classifier, the third term now plays an interesting role. The intuition is simple: the generator, conditioned on a class label, is supposed to sample an image. But if the generator creates really terrible images, then (hopefully) the classifier will be very confused and not be able to tell which class the generator was attempting to sample from. This thus encourages the generator to stay away from awful, hard-to-classify images and attracts it toward coherent, easy-to-classify images instead.
What Counts as Hard to Classify?
The ease with which the auxiliary classifier can accurately classify the generated images is exactly measured by the third term
\[\begin{align*} -\E_{p_\theta(x, y)}\brac{\ln q_\phi(y \mid x)}. \end{align*}\]But we can get a little more insight into the properties of this term by interpreting it as the variational upper bound of the generator’s conditional entropy \(H\_\theta(Y \mid X)\), whereby
\[\begin{align*} -\E_{p_\theta(x, y)}\brac{\ln q_\phi(y \mid x)} &= H_\theta(Y \mid X) + \E_{p_\theta(x)} \KL(p_\theta(y \mid x) \| q_\phi(y \mid x)), \end{align*}\]and where the conditional entropy is equivalently expressed as
\[\begin{align*} H_\theta(Y \mid X) = \E_{p_\theta(x)} \brac{ H(p_\theta(y \mid x)) }. \end{align*}\]Here, \(H(\cdot)\) denotes the entropy functional. This formulation shows that minimizing the original term actually consists of two parts: minimizing \(H\_\theta(Y \mid X)\) and making \(q\_\phi(y \mid x)\) a good variational approximation of \(p\_\theta(y \mid x)\). Images generated from the generator are thus easy to classify if and only if the following two conditions are met:
- \(\E\_{p\_\theta(x)} \brac{ H(p\_\theta(y \mid x)) }\) is minimized
- \(q\_\phi(y \mid x)\) is a good approximation of \(p\_\theta(y \mid x)\).
But recall that \(q\_\phi(y \mid x)\) is also trained to approximate \(p^*(y \mid x)\). This adds the third condition:
- \(\E\_{p\_\theta(x)} \brac{ H(p\_\theta(y \mid x)) }\) is minimized
- \(q\_\phi(y \mid x)\) is a good approximation of \(p\_\theta(y \mid x)\).
- \(q\_\phi(y \mid x)\) is a good approximation of \(p^*(y \mid x)\).
If you close one eye and squint the other, then you can sort of see that minimizing the AC-GAN objective implies minimizing \(\E\_{p_\theta} \brac{ H(p^*(y \mid x))}\). In other words, the generator is discouraged from sampling near the true decision boundary \(p^*(y \mid x)\).
Wait, What if the Images are Supposed to be Near the Decision Boundary?
If the generator down-samples images that are close to the decision boundary… what happens if the true density \(p^*(x)\) is concentrated near the decision boundary? Therein lies a fundamental problem with the AC-GAN objective. One of the reasons why AC-GAN performs well on visual inspection and Inception Score is because these metrics reward the generator for sampling easily-recognized images uniformly across the image classes. If, however, the true distribution \(p^*\) contains points that are fundamentally difficult to classify because they lie near the true decision boundary, then AC-GAN will down-sample these points and thus learn a biased distribution!
It shouldn’t come as too much of a surprise that AC-GAN down-samples points near the decision boundary. After all, being near the decision boundary, pretty much by definition, means the image is hard to classify. What is surprising, however, is how aggressively AC-GAN actually down-samples points near the decision boundary. To demonstrate this down-sampling behavior, I conducted two toy experiments.
Toy Experiment 1
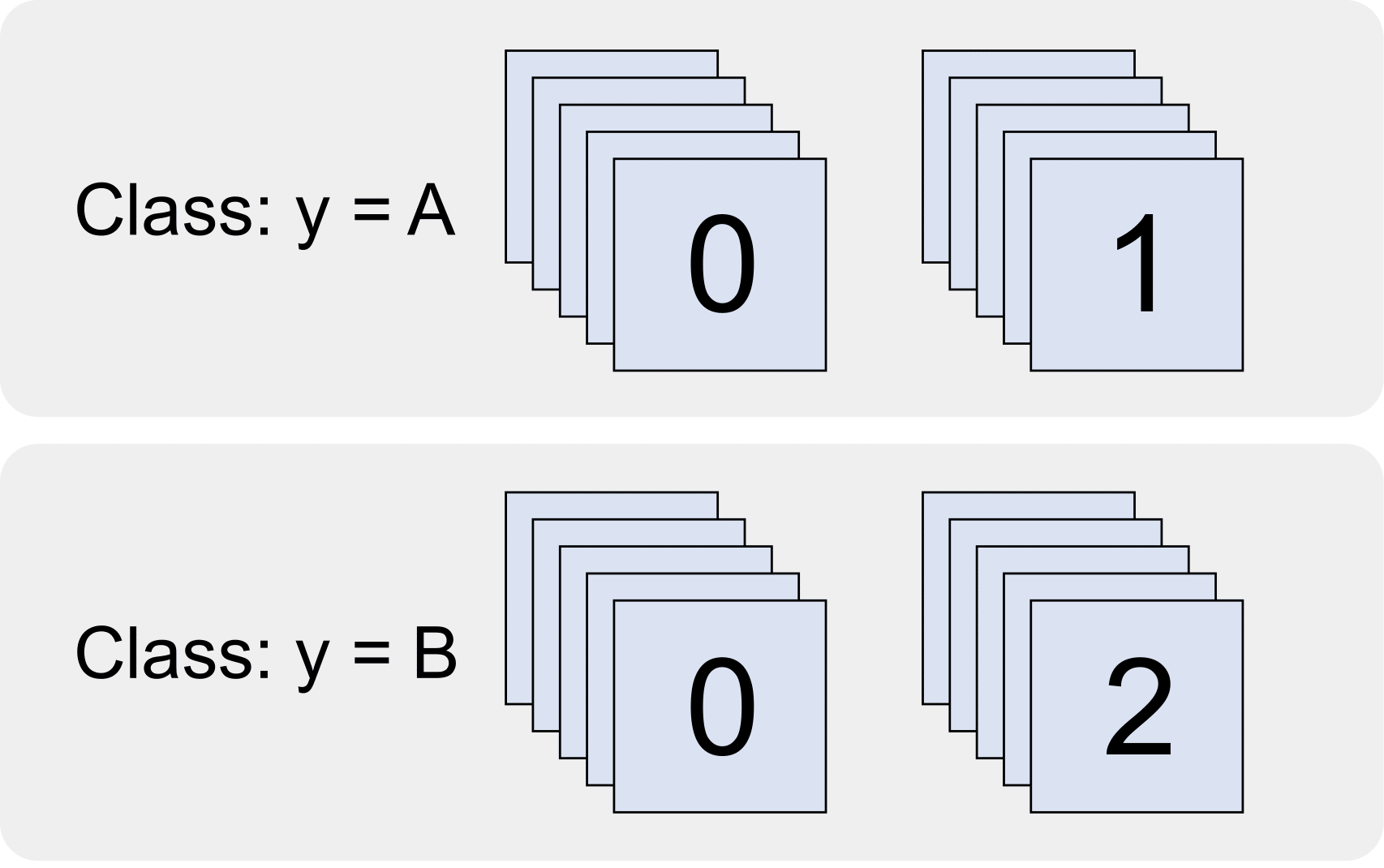
In the first toy experiment, I took the MNIST training set and constructed my own MNIST variant that contains only two classes: A and B. Class A only contains images of 0’s and 1’s, whereas class B only contains images of 0’s and 2’s. Because images of 0’s are as likely to belong in class A as class B, the all images of 0’s lie exactly in the decision boundary of the Bayes-optimal A/B classifier. If our analysis is correct, then AC-GAN ought to down-sample images of 0’s while successfully generating images of 1’s and 2’s. And indeed, that’s exactly what we see:

Here, I trained AC-GAN, which happens to contain a single binary latent variable. It turns out that we can easily convert the AC-GAN objective into the GAN or InfoGAN objectives:
- GAN Objective: AC-GAN Objective Term #1
- InfoGAN Objective: AC-GAN Objective Term #1 + #3
So I decided to train GAN and InfoGAN as well. In the above picture, \(\lambda\_m\) denotes the weighting of the third term. The greater the third term, the more we expect the model to down-sample points near the auxiliary classifier decision boundary. Because of this behavior, we see something quite interesting regarding how GAN, InfoGAN, and AC-GAN decides to leverage the binary latent variable.
The GAN objective function does not encourage the binary latent variable to be used in any particular way; all the GAN cares about is generating realistic images of 0’s, 1’s, and 2’s. And if the discrete latent variable isn’t useful, so be it.
The InfoGAN objective function also cares about down-sampling the points near the auxiliary classifier. However, InfoGAN is allowed to choose the behavior of the auxiliary classifier (and correspondingly, the behavior of the discrete latent variable). It therefore decided that the discrete latent variable and auxiliary classifier should work in tandem to associate A = {0} and B = {1, 2}. This way, all the images are far from the decision boundary.
The AC-GAN objective function, however, uses Term #2 to tie the behavior of the auxiliary classifier to the true class correspondences (where A = {0, 1}, and B = {0, 2}). As such, since images of 0’s lie in the Bayes-optimal decision boundary, and since auxiliary classifier is trained to approximate the Bayes-optimal decision boundary, images of 0’s are therefore near (or on) the auxiliary classifier decision boundary and thus down-sampled. Indeed, when \(\lambda\_m = 2\), the down-sampling is actually quite aggressive.

To quantify the down-sampling behavior, I computed the relative frequency of 0’s, 1’s, and 2’s as we increase the weighting of \(\lambda\_m\). We can see that the moment \(\lambda\_m\) becomes non-zero, the down-sampling behavior immediately starts occurring. And by the time \(\lambda\_m > 2\), AC-GAN almost never samples 0’s, despite 0’s making up 50% of the true image distribution!
Toy Experiment 2
To demonstrate this down-sampling behavior in a slightly less-contrived scenario, I trained AC-GAN on the original MNIST dataset. By doing so, something quite amusing becomes apparent: AC-GAN never generates a serifed 1!


It turns out that when you add protrusions to 1’s, it starts looking like a 2 (or possibly a 7). As such, serif 1’s are closer to the classifier decision boundary than sans-serif 1’s… and are therefore down-sampled. In other words:

I was pleasantly surprised with the experiment results and decided to convert it into a small submission to the Bayesian Deep Learning workshop. The submission includes additional experiments that demonstrate how AC-GAN can actually achieve a higher Inception Score than the original image distribution. From idea conception to paper submission, the entire process took a total of two days, which was the fastest I’ve ever completed a project! I also had a lot of fun making the poster, and even snuck SmileyBall into the end of it.