Autoencoding a Single Bit
Introduction
\(\newcommand{\E}{\mathbb{E}} \newcommand{\brac}[1]{\left[#1\right]} \newcommand{\paren}[1]{\left(#1\right)} \newcommand{\set}[1]{\left\{#1\right\}} \newcommand{\KL}{\text{KL}}\)
Here’s a seemingly silly idea: let’s try to encode a single bit of information with a variational autoencoder (VAE). Our data set thus consists of two i.i.d. samples. In fact, here’s what it looks like:
data = np.array([[0.],
[1.]])We will attempt to autoencoder this data using a variational autoencoder with a single-dimensional \(z\) (after all, one dimension should be sufficient), where \(p(z)\) is unit Gaussian, \(p(x \mid z)\) is Bernoulli, and \(q(z \mid x)\) is a conditional Gaussian—a standard formulation of the VAE.
To evaluate what the VAE is doing, we will monitor two metrics of interest: the reconstruction score \(-\ln p(x \mid z)\) and the KL-divergence \(\KL(q(z \mid x) \\| p(z))\) between the approximate posterior and the prior. Both the reconstruction score and the KL-divergence are indicators of how much information about \(x\) is encoded in \(z\). The more information is encoded, the higher the KL-divergence cost that we pay, but the smaller the reconstruction cost. So what behavior should we expect when we run our VAE?
*Drum roll*
Reconstruction cost: 0.693
KL cost: 0.0
Oh. Well that was anti-climactic. Remarkably, it looks almost like our VAE pretty much learned nothing about the data. It certainly encoded nothing into the latent variable \(z\)…
Wait, Why Did the VAE Fail?
If you buy into the beauty and power of the variational autoencoder, seeing the VAE fail so spectacularly can come as a shock at first. But once you’ve picked your shattered expectations off the ground, you’ll realize that this behavior is completely expected.
To be more precise, the VAE didn’t fail at all. In fact, the VAE learned to perfectly model the data by learning a very excellent Bernoulli decoder, where for all \(z\),
\[\begin{align*} p(x = 1 \mid z) &= 0.5 \\ p(x = 0 \mid z) &= 0.5 \end{align*}\]Furthermore, recall that the objective function of the VAE is to maximize the variational lower bound
\[\begin{align*} \ln p(x = 1) &\ge \E_{q(z\mid x = 1)} \brac{\ln p(z) p(x = 1 \mid z) - \ln q(z \mid x = 1)} \\ &= \E_{q(z \mid x = 1)} \brac{\ln p(x = 1 \mid z)} \\ &= -0.693. \end{align*}\]But \(\ln p(x = 1) = -0.693\) is the correct density since we in fact have one-half chance of sampling \(x = 1\). As such, we don’t have a lower bound: our VAE learned the actual density! Unfortunately, it’s just that our VAE found a way of modeling the data without using the latent variable \(z\) at all.
So the VAE Was Successful?
Well… yes and no. If your plan is to estimate the data density, then break out the champagne and celebrate this trivial accomplishment! You have successfully learned a model where the variational lower bound is tight (so tight that the gap is zero) and the model is exact :)
But if your plan is to learn a meaningful representation of the data… you have clearly failed D:
The Standard VAE Will Never Use the Latent Variable
If your plan is to learn a meaningful representation of the two-bit data, then you’re in a bit of a pickle. No matter how many times you run the VAE and how deep your neural networks, the VAE will consistently learn to encode zero information into \(z\) (which turns out to be the global optimum). This raises an important question: why exactly is the VAE so against encoding information into \(z\)? The reason has to do with our poorly chosen prior \(p(z)\) and approximate posterior \(q(z \mid x)\).
To facilitate our analysis, let’s look at another way to formulate our objective function. The usual objective is to maximize the variational lower bound,
\[\begin{align*} \ln p_\theta(x) \ge \E_{q_\phi(z \mid x)} \brac{\ln p_\theta(x, z) - \ln q_\phi(z \mid x)}. \end{align*}\]From a computational perspective, what we really care about is to estimate \(\theta\) via maximum likelihood. To make the generative model more expressive we make use of the latent variable \(z\), since
\[p(x) = \int p(x, z) dz\]has the potential to be arbitrarily complex. But this expressivity comes as a cost. Unfortunately, \(p_\theta(x)\) is intractable because marginalizing the latent variable \(z\) is potentially very challenging. So instead, we maximize the variational lower bound, which is computable. It should be easy to see that the higher the variational lower bound, the more density we assign to the data \(x\). But we can do a little bit of math to get yet another meaningful expression,
\[\begin{align*} \E_{q(z \mid x)} \brac{\ln p(x, z) - \ln q(z \mid x)} &= \E_{q(z \mid x)} \brac{\ln p(x) p(z \mid x) - \ln q(z \mid x)} \\ &= \ln p(x) - \E_{q(z \mid x)} \brac{\ln q(z \mid x) - \ln p(z \mid x)} \\ &= \ln p(x) - \KL(q(z \mid x) \| p(z \mid x)). \end{align*}\]The resulting expression isn’t very useful computationally, since \(p_\theta(z \mid x)\) is very difficult to compute. But it shows another side of the story to VAEs: maximizing the lower bound is exactly the same as maximizing the likelihood—provided that our variational approximation \(q(\cdot \vert \cdot)\) matches the true posterior \(p(\cdot \vert \cdot)\).
From this perspective, it is easy to see why our VAE did not use the latent variable \(z\). Note that not using the latent variable at all allows us to estimate the true density while matching the true posterior exactly (which is now simply the unit Gaussian prior—very easy to approximate). Let’s call this our default option. If we really want to use the latent variable, we will have to demonstrate an alternative option where,
- The latent variable is used.
- The model learns the true density.
- The approximate posterior exactly matches the true posterior.
Notice that all three conditions must be satisfied in order for there to even be a chance of the VAE learning to make sure of \(z\). However, it is easy to demonstrate that in all cases where \(z\) is used, the conditions can never be satisfied. Here is a quick proof.
A Proof by Contradiction
Suppose we have a model where the latent variable \(z\) is used, the model learns the true density, and the variational approximation matches the true posterior. Since the variational approximation matches the true posterior,
\[\begin{align*} p(z) &= \sum_{k = 0}^1 p(x = k) p(z \mid x = k) = \frac{1}{2} \sum_{k = 0}^1 p(z \mid x = k) \\ &= \frac{1}{2} \sum_{k = 0}^1 q(z \mid x = k). \end{align*}\]However, \(q(z \mid x = k)\) is a Gaussian and \((1/2) \sum_{k = 0}^1 q(z \mid x = k)\) is a mixture of two Gaussians. It is obvious that a mixture of two Gaussians can match \(p(z)\) if and only if
\[\begin{align*} q(z \mid x = 0) = q(z \mid x = 1) = p(z). \end{align*}\]However, this means we are not using the latent variable \(z\). We can conclude via proof by contradiction that our VAE will never use the latent variable \(z\). \(\Box\)
Forcing the Model to Use the Latent Variable
There is a way to force the model to use the latent variable. Instead of having a single dimensional data space, let’s use five dimensions, \(n=5\).
data = np.array([[0., 0., 0., 0., 0.],
[1., 1., 1., 1., 1.]])Here, we leverage the fact that our decoder generates the five dimensions independently when conditioned on \(z\). In other words,
\[\ln p(\mathbf{x} \mid z) = \sum_{i=1}^5 \ln p(x_i \mid z).\]Suppose we wish to learn to model this new data. If the model does not use the latent variable at all, the best we can do is to set \(\ln p(x_i \mid z) = 0.5\) for all \(x_i\) and \(z\). Unfortunately, this means \(\ln p(\mathbf{x}^{(0)}) = \ln p(\mathbf{x}^{(1)}) = -3.47\), which is a far ways off from the true density \(-0.693\). The fact that the decoder generates the five dimensions independently now puts stress on model to rely on the latent variable \(z\) to coordinate the five independent dimensions.
By increasing the value of \(n\), we put increasing pressure on the model to use the latent variable, which we can monitor by looking at the reconstruction cost per dimension.
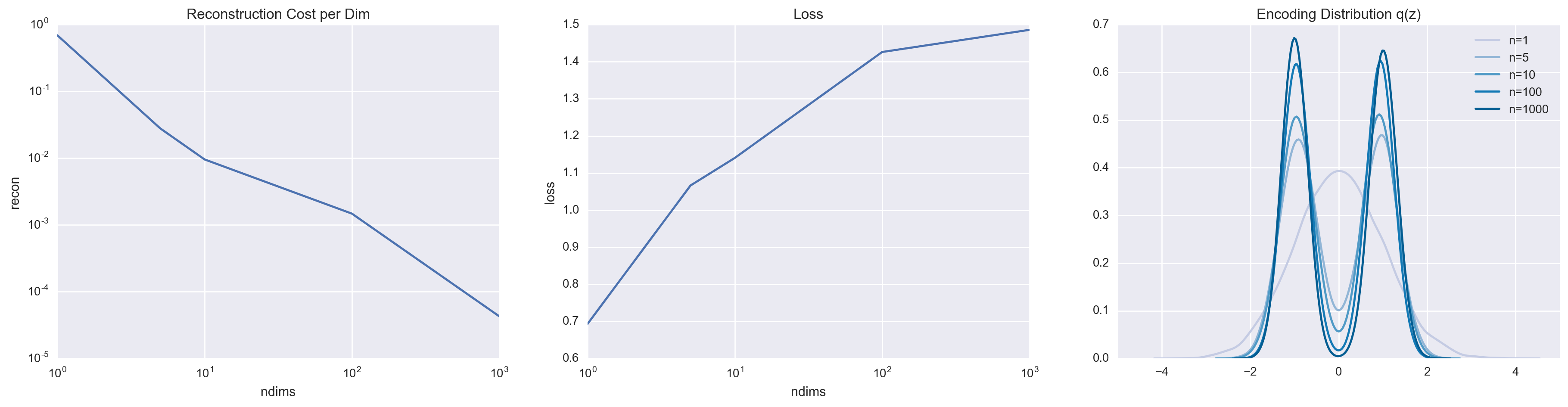
But we shouldn’t start high-fiving ourselves yet just because we’re able to force \(z\) to be meaningful. This ability to minimize the per-dimension reconstruction cost comes at a hefty cost. Remember that we are limiting ourselves to the family of Gaussians for our variational approximation. Because we are now increasingly forced to rely on the latent variable, we are forced to pay the \(\KL(q(z \mid x) \\| p(z \mid x))\) price, which raises our loss. This is best visualized by looking at the encoding distribution, which we define as,
\[q(z) = \sum_{k = 0}^1 \frac{1}{2} q(z \mid x).\]Simply by visual inspection, it is easy to see that the encoding distribution fails to match the prior. Furthermore, it tends to be the case that a poor variational family (in our case, the family of Gaussians) leads to a poor generative model. In this case, note that the highest density is at \(z = 0\). This unfortunately coincides with the valley of \(q(z)\). So what is \(p(x \mid z = 0)\)? More likely than not, it is going to be some unpleasant average of the two data points.
Encoding Without the Price
One of the key take-home messages is that, because our variational family is imperfect, we will always pay a price when encoding into \(z\). Failure to match the true posterior leads to a poorer variational lower bound, which usually means a poorer maximum likelihood on the training set, which usually means a poorer maximum likelihood on the test set, which implies a poorer generative model.
Much of VAE research has thus beeen dedicated to improving the variational lower bound by expanding the variational family beyond the set of Gaussians. It turns out that one very simple way of doing so is by simply using a Deep Latent Gaussian Model (DLGM) and using structured inference. In other words, we shall use the following generative model,
\[p(z_2, z_1 , x) = p(z_2) p(z_1 \mid z_2) p(x \mid z_1),\]and the following inference model,
\[q(z_2, z_1 \mid x) = q(z_1 \mid x) q(z_2 \mid z_1).\]Although we are still sticking to Gaussians for all of the factorized distributions, it is worth noting that \(q(z_2 \mid x)\) is potentially an arbitrarily complex distribution since we get to marginalize over the latent variable \(z_1\). This gives us a better shot of matching true posterior, provided that we’re lucky enough that \(p(z_1 \mid x)\) is actually Gaussian.
In the case of our 1-bit data, this actually seems plausible. We consider the following generative model:
\[\begin{align*} p(z_2) &= \mathcal{N}(z_2 \mid 0, 1)\\ p(z_1 \mid z_2 \le 0) &= \mathcal{N}(z_1 \mid -a, 1)\\ p(z_1 \mid z_2 > 0) &= \mathcal{N}(z_1 \mid a, 1)\\ p(x = x^{(0)} \mid z_1 \le 0) &= 1 \\ p(x = x^{(1)} \mid z_1 > 0) &= 1. \end{align*}\]If we set \(a\) to be really big, then it is approximately true that \(z_2 \le 0\) maps to \(x^{(0)}\) and \(z_2 > 0\) maps to \(x^{(1)}\). By focusing on \(x^{(0)}\), we can easily determine what the true posteriors ought to be.
Notice that \(p(z_1)\) is a mixture of two Gaussians. Since \(x^{(0)}\) is almost always generated from the first Gaussian component \(p(z_1 \mid z_2 \le 0)\), the true posterior for \(p(z_1 \mid x^{(0)})\) will approximately be the same as \(p(z_1 \mid z_2 \le 0)\). Similarly, since \(x^{(0)}\) is almost always generated from \(z_2 \le 0\), the true posterior for \(p(z_2 \mid x^{(0)})\) will approximately be a truncuated Gaussian (the left-half of the prior \(p(z_2)\)). Of course, these are only approximations, but it turns out that these approximations are good enough!
We can set \(n = 1000\) (this really forces the VAE to encoding using the latent variables) and take a look at how good a 1-layer VAE and a 2-layer VAE are at matching the prior distributions \(p(z)\) and \(p(z_2)\) respectively.
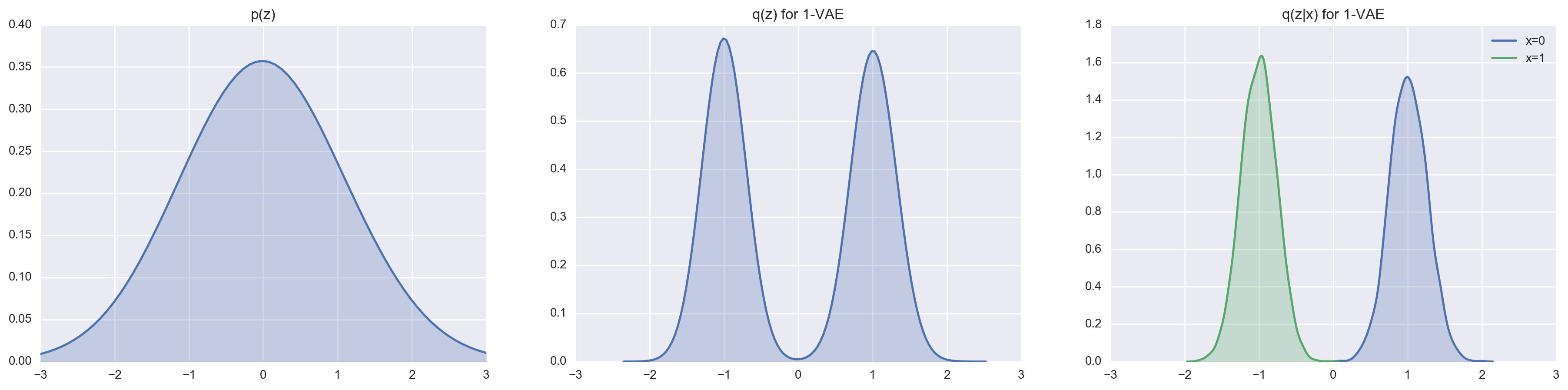
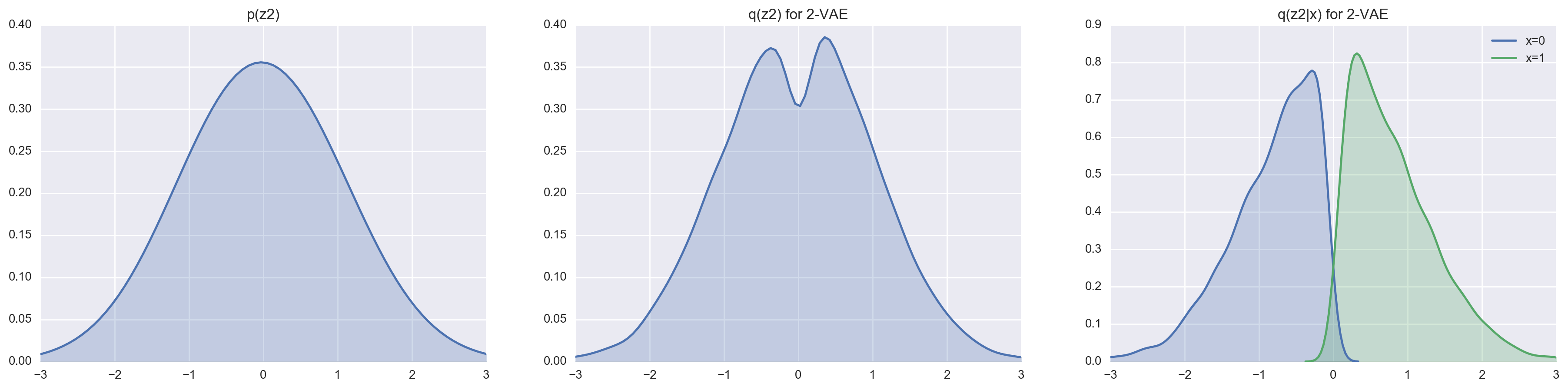
In comparison to the 1-layer VAE, the 2-layer VAE is a lot more capable at approximating the truncuated Gaussian posterior thanks to the marginalization of the latent variable \(z_1\). We can most easily see this by comparing the reconstruction cost and loss.
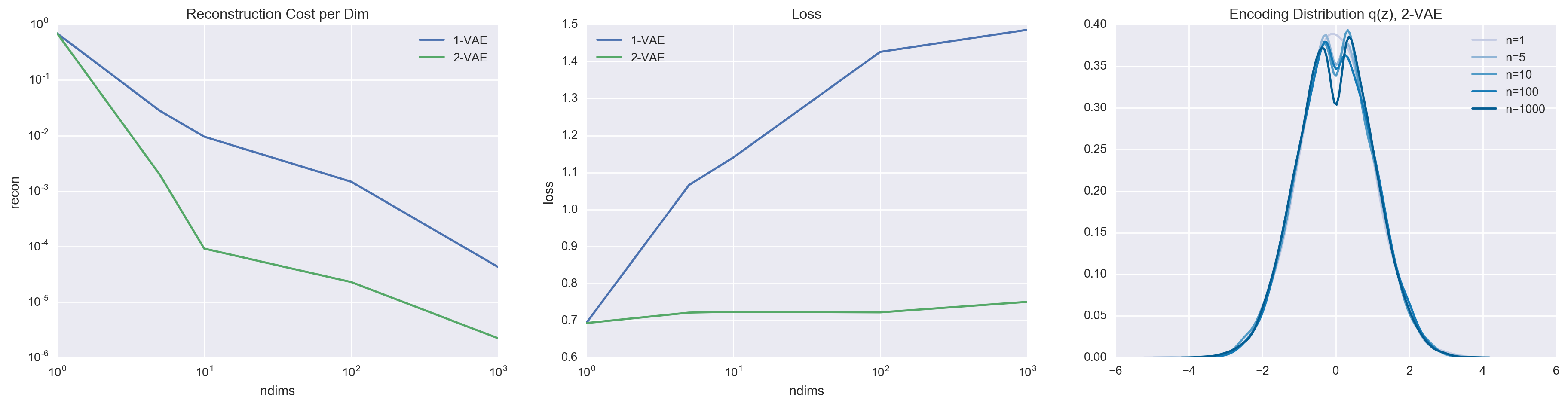
It is easy to see that the 2-layer VAE achieves better reconstruction cost and lower loss. All of this is thanks to the more expressive variational family, which enabled \(q(z_2 \mid x)\) to be a complex distribution (in this case, approximating a truncated Gaussian). It is also worth noting that the 2-layer VAE isn’t perfect (it also fails to exactly match the true posterior). This is why when \(n = 1\), both VAEs default to not using the latent variable whatsoever.
Do Not Do this at Home. Or Anywhere.
There’s an excellent saying that:
If all you have is a hammer, everything looks like a nail.
Given the simplicity of the data sets (regardless of the number of dimensions \(n\)) that we are considering, there are much simpler models that can perfectly learn the true data density. So before you start using your deep amortized variational hammer on every task available, it is always wise to ask yourself whether a different (preferably simpler) tool can do the job equally well, if not better.
Silly, but Hopefully Insightful!
Disclaimers aside, it is worth realizing that when \(n > 1\), the standard VAE does need the latent variable and actually fails to learn the correct density. This simple exercise reveals some of the consistency issues that the VAE experiences—an issue that continues to plague VAE on more complex tasks if your variational family is misspecified (relative to your choice of generative model and the true data-generating distribution). By reducing to the simplest possible example, we get to see this limitation play out.
Personally, I think seeing the 2-layer VAE approximate a truncated Gaussian is also really exciting! I have long suspected this behavior, but seeing is believing, right?
I hope this post can serve as a (weak) counter-point to the \(\beta\)-VAE paper. After all, this post provides a counter-example (albiet a very contrived one) where you have to give the reconstruction term higher weight in order to force the encoding representation to be meaningful. If someone can find a less trivial counter-point, that would be quite interesting!
If you want to learn more about some of the stuff described in this post, I highly recommend Peter Chen’s Variational Lossy Autoencoder paper and Matt Hoffman’s ELBO surgery paper!
And last but not least, here’s some code :D